안녕하세요 기린입니다 :)
지난 시간까지 선택 정렬, 버블 정렬, 삽입 정렬, 퀵 정렬 알고리즘을 공부했습니다. 이번에는 병합 정렬 (Merge Sort)에 대해 알아보겠습니다 !
병합 정렬도 퀵 정렬 알고리즘과 같이 '분할 정복' 방법을 채택한 알고리즘 인데요 결론은 시간 복잡도가 O(N * logN)이라는 거죠 :]
다만 퀵 정렬 알고리즘은 피벗 값에 따라서 편향되게 분할할 가능성이 있다는 점에서 최악의 경우 O(N ^ 2)의 시간 복잡도를 가지지만 병학 정렬 알고리즘은 정확히 반절씩 나눈다는 점에서 최악의 경우에도 O(N * logN)의 시간 복잡도를 보장합니다. 퀵 정렬을 이해하셨다면 이 병합 정렬은 쉽게 이해하실 수 있을겁니다.
다음의 숫자들을 오름차순으로 정렬하는 프로그램을 작성하세요.
8 2 6 5 3 1 4
병합 정렬은 하나의 큰 문제를 두 개의 작은 문제로 분할한 뒤에 각자 계산하고 나중에 합치는 방법을 채택합니다.
즉, 일단 정확히 반으로 나누고 나중에 정렬 하는 것입니다.
반으로 나누고 나중에 정렬... 어떻게 해야할지 쉽지않아 보이죠 ?? 위 문제를 푸는 소스 코드부터 보시죠
#include <stdio.h>
int number = 8;
int sorted[8]; // 정렬 배열은 반드시 전역 변수로 선언하면 공통된 메모리를 사용할 수 있다.
void merge(int a[], int m, int middle, int n) {
int i = m;
int j = middle + 1;
int k = m;
// 작은 순서대로 배열에 삽입
while (i <= middle && j <= n) {
if (a[i] <= a[j]) {
sorted[k] = a[i];
i++;
} else {
sorted[k] = a[j];
j++;
}
k++;
}
// 남은 데이터도 삽입
if (i > middle) {
for (int t = j; t <= n; t++) {
sorted[k] = a[t];
k++;
}
} else {
for (int t = i; t <= middle; t++) {
sorted[k] = a[t];
k++;
}
}
// 정렬된 배열을 삽입
for (int t = m; t <= n; t++) {
a[t] = sorted[t];
}
}
void mergeSort(int a[], int m, int n) {
// 크기가 1개인 경우
if (m < n) {
int middle = (m + n) / 2;
mergeSort(a, m, middle);
mergeSort(a, middle + 1, n);
merge(a, m, middle, n);
}
}
int main(void) {
int array[number] = {8, 2, 6, 5, 3, 1, 6, 4};
mergeSort(array, 0, number - 1);
// 출력
for (int i = 0; i < number; i++) {
printf("%d", array[i]);
}
}먼저, merge 함수는 정렬 후 합치는 과정을 수행합니다 그리고 mergeSort 함수는 재귀함수로 정확히 반을 나누는 역할을 한다고 볼 수 있죠. 하나씩 살펴보도록 할게요 :]
메인 함수에서 mergeSort(array, 0, number - 1) 가 실행됩니다. 여기서 파라미터 값은 array 는 8, 2, 6, 5, 3, 1, 6, 4 인 배열이 들어가고 파라미터 m 에 0, n 에 7 이 들어갑니다
첫 번째 조건문인 if 문 if (m < n) 의 의미는 크기가 1이 될 때까지 재귀함수가 실행되도록 하는것이죠
조건문 안에는 절반을 나누기 위한 middle 값을 구하고 1. mergeSort(a, m, middle) 과 2. mergeSort(a, middle + 1, n) 가 실행되는데요 각 함수는 middle을 기준으로 정확히 반으로 나눈후 재귀하는 역할을 하고 있습니다. 그리고 merge(a, m, middle, n) 함수가 실행되는데 이 함수는 정렬 후 합치는 과정을 수행하는데 자세히 보실게요.
첫 번째 단계에서는 크기가 개별 배열인, 즉 크기가 1인 배열 상태로 시작합니다

구체화 하자면 위 그림에서 시작 열과 같이 각 원소가 크기가 1인 상태로 나열되어 있는걸 확인하실 수 있습니다. 해당 열을 mergeSort 함수 파라미터로 넘기면 어떻게 수행되는지 확인해보겠습니다.
먼저, middle 값은 정수값으로 (0 + 7) / 2 = 3 이 되고 1. mergeSort(a, m, middle) 함수가 수행되는데
a 값과 m 값은 그대로 들어가지만 middle 값이 3이므로 기존에 7에서 3으로 변경되겠죠 즉,

처음 mergeSort 함수가 실행 됐을때 m값과 n값이 이랬다면
함수안 조건문에 있는 1.mergeSort(a, 0, 3) 은

이렇게 정확히 반을 나누어 지게됩니다. 그리고 재귀함수이기 때문에 다시 조건문 안에 있는 mergeSort(a, 0, 1) 이 실행되겠죠 ? 헷갈리시는 분이 계시다면 소스코드를 보며 하나씩 손코딩 해보시길 추천드립니다

정확히 반을 나누어 프로그램이 실행되고 있는게 보이시죠 ? 이제 mergeSort(a, 0, 1) 함수 안에 있는 조건문 속 두 개의 재귀함수 mergeSort는 middle 값이 0이 되므로 조건문이 실행되지 않기 때문에 예외처리가 될 것이고 드디어 첫 merge함수가 실행됩니다. 즉, merge(a, 0, 0, 1) 이 실행되겠죠
void merge(int a[], int m, int middle, int n) {
int i = m;
int j = middle + 1;
int k = m;
...
}변수를 보시면 i 는 0, j 는 1, 그리고 k 는 0 으로 선언 합니다.
// 작은 순서대로 배열에 삽입
while (i <= middle && j <= n) {
if (a[i] <= a[j]) {
sorted[k] = a[i];
i++;
} else {
sorted[k] = a[j];
j++;
}
k++;
}그 다음 while 문을 보시면 i 부터 middle 까지 그리고 j 부터 n 까지 작은 순서대로 정렬하여 배열에 삽입하도록 되어있습니다.
실제로 값을 넣어보겠습니다.

여기서 middle 값이 0, n 값이 1 이므로 조건이 성립하기 while 문이 실행되고 그 안에서 a[i] 값과 a[j] 값을 비교하여 sorted[k] 자리에 입력하죠. 그리고 while 문이 종료된 후 나머지 빈칸에 값을 넣는 프로그램이 필요합니다
// 남은 데이터도 삽입
if (i > middle) {
for (int t = j; t <= n; t++) {
sorted[k] = a[t];
k++;
}
} else {
for (int t = i; t <= middle; t++) {
sorted[k] = a[t];
k++;
}
}여기서도 정확하게 반을 나누어 삽입하는데요 i 가 middle 보다 크다면 즉, 왼쪽 반이 먼저 정렬이 끝난거면 오른쪽 값을 배열에 입력하고 그게 아니라면 왼쪽 값을 배열에 그대로 입력하게 되는거죠. 그리고 마지막으로
// 정렬된 배열을 삽입
for (int t = m; t <= n; t++) {
a[t] = sorted[t];
}정렬이 된 배열을 삽입하는데, 다시 말해 정렬과 합치는 과정을 동시에 진행하는거죠
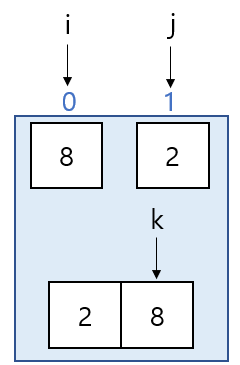
결과는 위와 같습니다 이런식으로 쭉 연산을 하다보면

두번째 연산은 이렇게 진행되겠죠 ? 반으로 나누어 정렬과 동시에 병합 합니다.
마지막 세번째 연산까지 하게되면 아래와 같이 과정을 표현할 수 있겠네요.
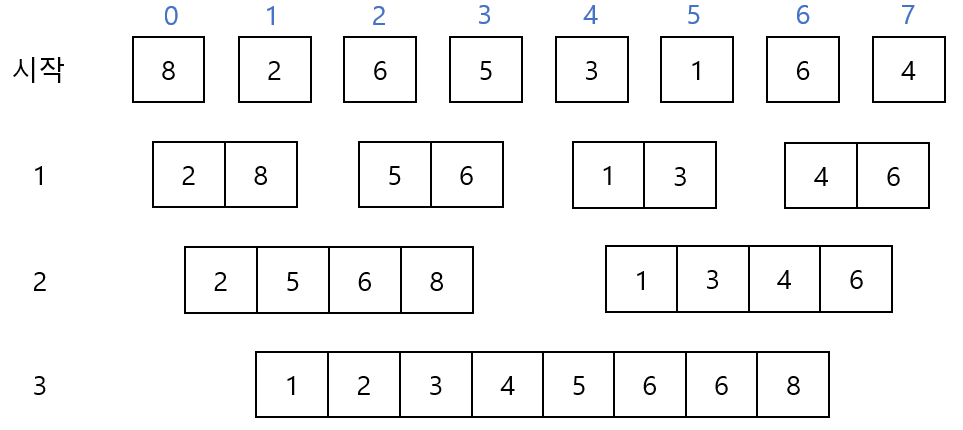
시작부터 마지막 세 번째 연산까지 진행해봤는데요 여기서 중요한 점이 있습니다.
연산을 할 때마다 정렬과 병합을 동시에 하게되는데 여기서 정렬은 정확히 8번을 수행하고 병합은 3번을 수행하게 됩니다. 왜냐하면 합치는 갯수가 2배씩 증가한다는 점에서 2 ^ 3 = 8 이므로 3단계만 필요하고 단계의 크기는 단계별로 정렬 후 병합하므로 데이터의 갯수와 동일하다고 생각하시면 됩니다. 결과적으로 병합 정렬의 시간 복잡도는 O(N * logN)이라고 할 수 있습니다.
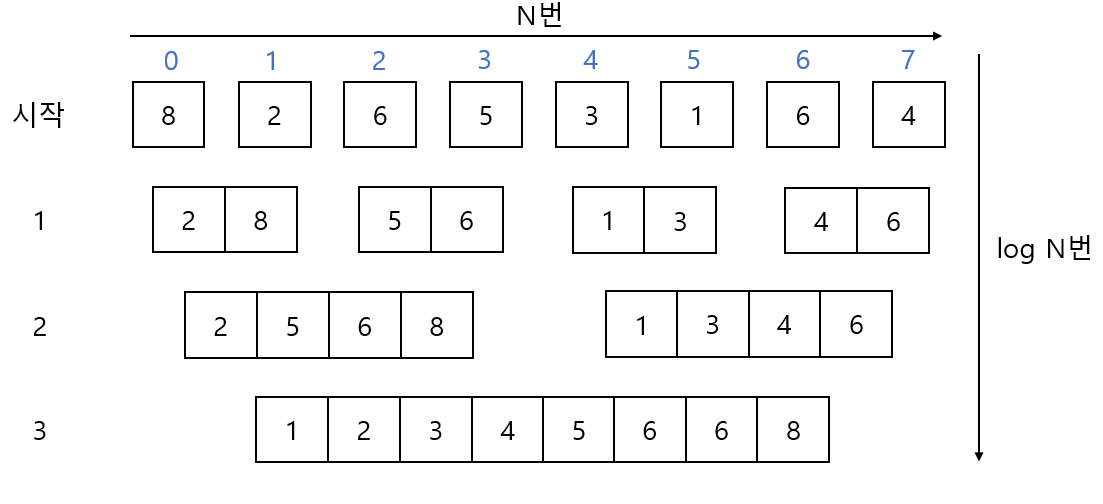
다시 말해 단계별로 정렬하고 병합하기 때문에 다음 단계에서 이미 정렬되어 있는 두 개를 합치는 것은 시간 복잡도 O(N)이면 충분하기 때문이죠 :) 이해되셨나요 ?
병합 정렬을 구현할 때 반드시 정렬에 사용되는 배열은 '전역 변수'로 선언해야 한다는 것인데요. 함수 안에서 배열을 선언하면 매 번 선언을 해야한다는 점에서 메모리 낭비가 커질 수 있으니까요 :] 따라서, 병합 정렬은 시간 복잡도 O(N * logN)을 보장해주지만 기존의 데이터를 담을 추가적인 배열 공간이 필요하다는 점에서 메모리 활용이 비효율적이라는 문제가 있습니다. 또한, 일반적인 경우 퀵 정렬보다 느리지만 어떤 상황에서도 정확한 시간 복잡도를 보장할 수 있다는 매우 효율적인 알고리즘입니다.
자 그럼 즐거운 코딩하세요 !
문의: ralla0405@gmail.com



